
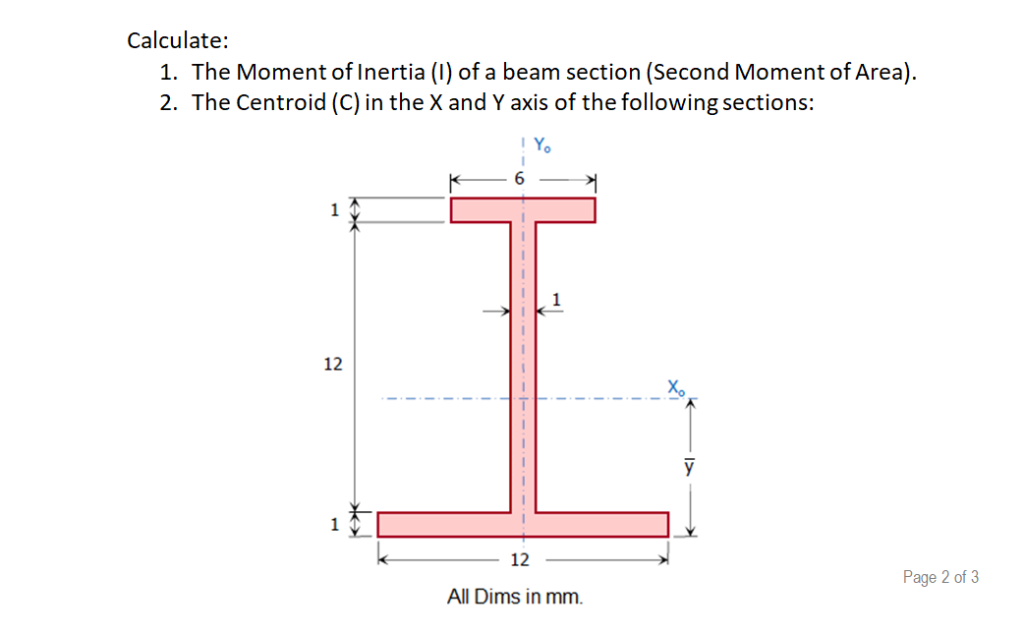
To calculate the moment of inertia of such a beam, it is necessary to split it into two identical pieces and sum the individual moments of inertia about the centroid of the complete structure, using the following equation: Double T Beam Moment Of InertiaĪ double T beam is made up of three plates, as shown in the following figure: Using the same T beam, the moment of inertia about the y-axis is as follows: Extension Of T Beam Moment Of Inertiaīeginning with the moment of inertia of a T beam, there are further extensions, which are introduced below. Therefore, the moment of inertia of section A is calculated as follows:Īnd the moment of inertia of section B is calculated as follows:įinally, adding the two together, the total moment of inertia of the T beam is calculated as follows: Example Calculation To calculate the moment of inertia of a T beam about its y-axis, the beam must again be divided into two sections, as follows:
To calculate the moment of inertia about the x-axis, the following steps are taken: To demonstrate the calculation of the moment of inertia about the x-axis for a T beam, assume a T beam with the following dimensions: Using the above equation, the centroid of the entire beam is calculated using the individual centroids of the components that the beam was split into. To calculate the value of ȳ c, the following equation is used: ȳ c is the centroid of the entire beam, with SI units of mm.ȳ i is the centroid of the i-th part of the T beam, with SI units of mm.In the case of a T beam, the centroidal axis is ȳ c, so the distance between the two axes can be calculated with the following equation: To apply the parallel axis theorem to calculate the moment of inertia of a T beam, the first step is to determine the distance between the two axes, I x’and I x. d is the distance between the two axes, with SI units of mm.A is the cross-sectional area beam, with SI units of mm 2.
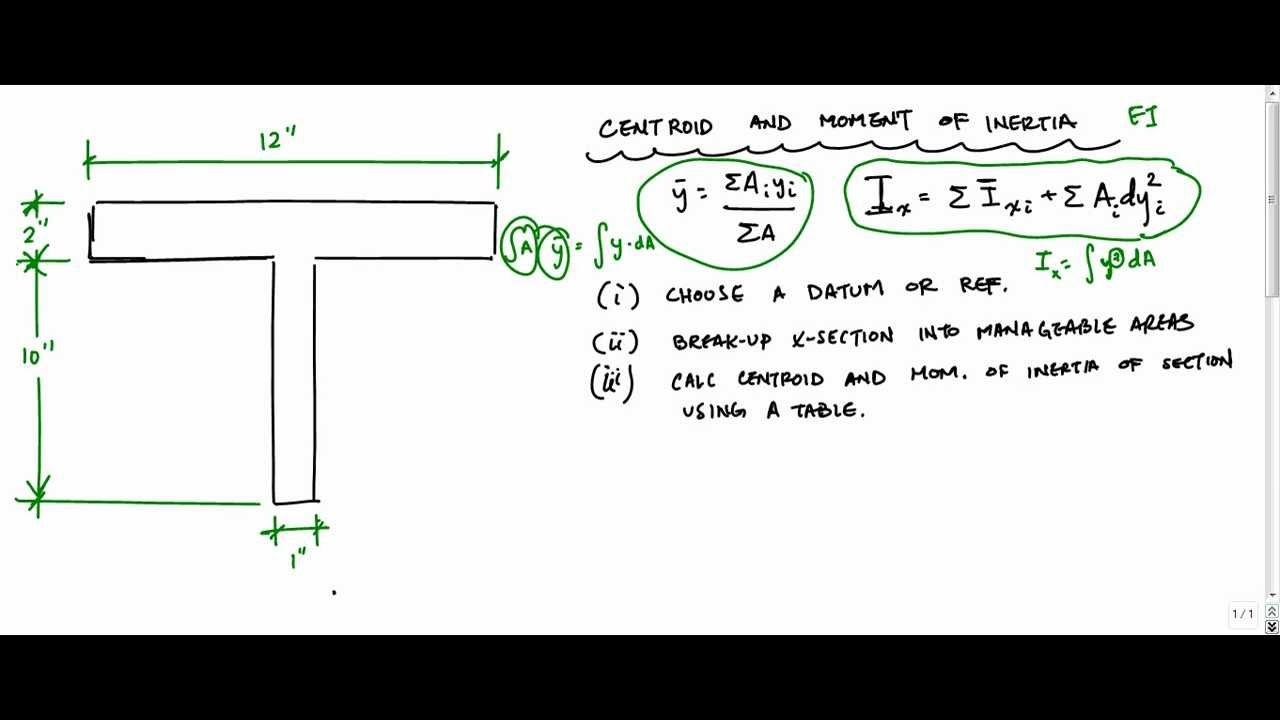
I is the moment of inertia about the centroid axis, with SI units of mm 4.I’ is the moment of inertia about the non-centroid axis, with SI units of mm 4.The parallel axis theorem specifies that the moment of inertia about a non-centroid axis can be calculated using the moment of inertia about a centroid axis, so long as the two axes are parallel. In that case, the moment of inertia about the x’-axis, I x’, will have SI units of mm 4. Note that in common engineering applications, the dimensions of a T beam may be given in mm. t f is the thickness of the flange, with SI units of m.b is the width of the flange, with SI units of m.h is the height of the beam, with SI units of m.t w is the width of the thickness of the web, with SI units of m.The moment of inertia of a T beam about the x’-axis is calculated using the following equation: To calculate the moment of inertia of a T beam about the x-axis, it is necessary to divide the section into two pieces, as shown in the following figure:īecause a T beam is not symmetric about the x-axis, it is necessary to calculate the moment of inertia about the x’-axis, and use the parallel axis theorem to determine the moment of inertia about the x-axis. Application Of The Moment Of Inertia Of A T Beam.


 0 kommentar(er)
0 kommentar(er)
